© 2025 Jerry Rabow. All Rights Reserved. Privacy Policy | Terms of Use
Contact me:
JerryRabow@JerryRabow.com
JerryRabow@JerryRabow.com

PUZZLES

I’ve always been interested in puzzles, and recently I’ve been experimenting with calculating, designing, and fabricating some interesting geometric puzzles. These puzzles are based upon a branch of recreational mathematics called Geometric Dissections. In its pure form, a Geometric Dissection requires that you start with a specified regular geometrical plane shape (a square, a pentagon, etc.), and the challenge is to devise the simplest and most elegant way to divide the original shape, using straight cuts, into the fewest number of pieces that can be reassembled to also form a different specified regular geometric shape. This can be very difficult, often requiring complex mathematics and repeated trial-and-error attempts.
But once a pure dissection problem has been solved by someone else who has discovered the individual pieces, it can still provide the rest of us the challenge of seeing if we can reassemble those pieces into the two specified regular geometric shapes. So far, I’ve been working only with shapes called “regular polygons.”
|
●
|
A polygon is “regular” when all sides have equal length and all outside angles are equal.
|
|
●
|
Regular polygons include both a convex polygon (like a stop sign [octogon]), and a star polygon sometimes called a polygram (like the star [pentagram] in the American flag):
|

The rules for the puzzles are simple: You must use all of the pieces, and they all have to be placed face up (in the puzzles that I’m making, the bottom of each piece is flat but there is a ridge along the top edges). And, of course, I hope everyone follows the basic rule of puzzles: It’s very good to share puzzles with friends; it’s very bad to share solutions.
My contribution to making these dissection puzzles is to minimize reliance upon some higher order mathematics by using the built-in math and measurement powers in Computer Assisted Drawing (CAD) software. And since some CAD software can output files in 3D printer instruction format, I can then fabricate the puzzle pieces on a 3D printer with reasonable precision and durability.
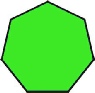
I’ve completed a set of four puzzles so far, and hope soon to share these, and additional and more complex future puzzles, by online posting of exact dimensions for home construction. If there is some interest, I might also be able to produce these puzzles for the public. All of my first four puzzle sets make a square as one of their alternate shapes. The other regular polygon shapes made with these puzzles are a Hexagram (6-pointed), a Pentagram (5-pointed), a Heptagon (7 sided), or a Decagon (10-sided) :
As soon as I have a chance, I plan to post more information about these puzzles on this webpage, including diagrams and measurements of the puzzle pieces for readers who want to hand-craft the puzzles themselves, tips on using CAD software and a 3D printer to make these puzzles, some background information on the history of Geometric Dissections, acknowledgment of the enthusiasts who devised some of these remarkable dissections, and a bibliography of further resources.
I’ve completed a set of four puzzles so far, and hope soon to share these, and additional and more complex future puzzles, by online posting of exact dimensions for home construction. If there is some interest, I might also be able to produce these puzzles for the public. All of my first four puzzle sets make a square as one of their alternate shapes. The other regular polygon shapes made with these puzzles are a Hexagram (6-pointed), a Pentagram (5-pointed), a Heptagon (7 sided), or a Decagon (10-sided) :
As soon as I have a chance, I plan to post more information about these puzzles on this webpage, including diagrams and measurements of the puzzle pieces for readers who want to hand-craft the puzzles themselves, tips on using CAD software and a 3D printer to make these puzzles, some background information on the history of Geometric Dissections, acknowledgment of the enthusiasts who devised some of these remarkable dissections, and a bibliography of further resources.
Meanwhile, if you have any questions, comments, or suggestions about my Geometric Dissection puzzles, please email me: JerryRabow@JerryRabow.com
Octogon
Pentagram